Introduction
학교 교육은 기본적으로 모든 학생에게 적합한 교육 기회의 제공을 목적으로 하고 있으며, 이는 학생들에 게 어떤 학습 기회가 제공되는가에 따라 학생들의 수학적 사고 수준과 성취가 달라지기 때문이다(Son et al., 2020). 그러나 수업을 통한 교육 기회의 제공은 단순히 평등과 균등의 개념이 아니라 복합적인 인지활동이 므로(Cha et al., 2020), 학생의 특성과 사회 계층 간 교육 격차, 소득과 같은 여러 요인들을 함께 고려해야 한다. 학생들의 교육 기회 보장을 위해 고려해야할 여러 요인들 중 학습부진은 심각하게 논의되어야할 부적응 문 제이다. 학습부진은 시험불안, 공부 자체에 대한 회의, 성적에 대한 걱정, 학습 환경 등의 다양한 맥락과 연결 되며, 후속 학습에 영향을 미치므로 관련된 이론적 배경을 고려해야할 뿐만 아니라 다각적인 차원에서의 접 근이 필요하다(Kim, 2001).
학습부진은 여러 교과에서 발생하지만, 수학의 경우 학습과정이 위계적 특성을 지니므로 학습 결손의 누 적이 심각한 수준으로 발전할 수 있는 가능성을 지닌다(Kim, 2001). 이로 인해, 수학학습부진은 학습부진아 의 비율이 다른 교과에 비해 높은 교과이며, 학교 현장에서는 다양한 수학학습부진아들이 모든 학년에 걸쳐 발생하고 있는 실정이다(Park & Oh, 2013). 또한 수학학습부진은 단지 한 가지 요인으로 인해 발생하는 것이 아니라 여러 요인들의 복합적인 상호작용으로 발생하므로 한 번 수학학습부진아가 되면 벗어나기 어려운 교과로 인식되고 있다(Yang & Kim, 2018).
이러한 이유로 그동안 수학학습부진에 대한 연구는 다양한 각도에서 이루어져 왔다. 구체적으로 살펴보 면, 수학을 학습하는데 어려움을 가진 학생들을 지원하기 위한 중재 효과(Lee et al., 2014; Yoon et al., 2014), 수 학학습부진아의 특성(Nam & Park, 2008; Yi et al., 2002), 교수 방법의 효과 분석(Kim & Oh, 2010; Lee & Park 2015) 등이 있다. 그러나 수학학습부진 연구가 현재까지 어떻게 이루어져 왔는지 그리고 부족한 연구는 무엇 인지에 대한 연구 동향을 밝힌 연구는 거의 수행되지 않았다. 수학학습부진 학생에 대한 수학중재 연구 동향 을 밝힌 Jo & Hong (2018)의 연구와 협동학습과 또래교수 프로그램이 수학학습부진아의 인지적 · 정의적 영 역에 미치는 효과를 메타분석한 Lee & Ko (2015)의 연구 등이 있으나, 특정 주제에 초점을 맞추었을 뿐만 아 니라 연구 대상이 일부 문헌에 한정되어 있으므로 국내 수학학습부진 연구의 전반적인 동향을 파악하기에 는 한계가 있다. 또한 분석과정이 연구자의 손으로 이루어지므로 대량의 문헌을 분석하는데 오랜 시간과 노 력이 필요할 뿐만 아니라 연구자의 주관성을 배제하지 못한다는 제한점이 있다(Son & Lee, 2020). 이러한 제 한점을 벗어나 데이터의 효율적인 처리와 그 이면에 감춰진 의미를 밝힐 수 있는 기법 중 하나는 토픽모델링 (topic modeling)이다(Blei & Lafferty, 2009). 토픽모델링을 통해 연구자의 주관성을 대폭 배제하고 데이터 처리 와 의미 파악에 드는 시간과 노력을 줄일 수 있다(Blei et al., 2003).
이에 본 연구에서는 토픽모델링을 활용하여 국내 수학학습부진 연구 동향을 분석하였다. 현재까지 이루어 진 수학학습부진 연구가 어떻게 분류되고 흘러왔는지 파악함으로써 향후 수학학습부진 연구에 대한 교육적 시사점을 제시하고자 한다.
Theoretical Background
Concept and Causes of Mathematics Struggling Learners
학습부진아는 개인이 가진 능력에서 기대한 성취에 도달하지 못한 학생을 의미하며, 신경 장애와 뇌손상과 같은 신체적 혹은 정보 처리 과정의 장애로 인해 학습의 부적응을 보이는 학습 장애와는 다르다(Kim, 2001). 즉, 신체적이나 정신적인 장애가 없고 정상적인 학교생활을 영위할 수 있는 학업 잠재력을 지니고 있으나 영향을 미치는 여러 요인들로 인해 교육과정에서 요구하는 기본적인 학업 수준에 도달하지 못한 학습자를 의미한다(Park & Oh, 2013). 이러한 특성에 따라 한국교육과정평가원(1998)에서는 수학학습부진을 교육과정에서 제시한 최저 수준의 목표를 도달하지 못한 학생으로 정의하며, 단위 학교에서는 수학교과에 대한 진단 평가에서 기초학력미달 학생을 수학학습부진아라 일컫는다. 본 연구에서는 학습부진아와 학습장애를 구분하고 학습부진아에 대한 연구만을 분석 대상으로 선정하였다.
수학학습부진의 원인은 다양하고 복합적이나 크게 나누어보면 학생 변인, 수업 변인, 사회문화 변인, 수학 변인으로 구분할 수 있다(Kim, 2001). 먼저 학생 변인은 선행학습의 결손, 학습방법의 미숙 언어와 수리 등 기초능력의 부족과 같은 인지적 요인과 학습의욕 및 흥미 부족, 자신감 결여, 부정적 자아 정체감, 정서 불안, 집중력 부족, 수학 불안 등의 정의적 요인으로 구분할 수 있다. 다음으로 수업 변인은 내용 요인과 교사 요인이 있으며, 내용 요인의 경우 학습내용이 너무 많거나 학습내용이 연역적으로 구성되어 형식적인 수학을 이해하기 어려운 수학 학습 부진아들에게 학습 결손을 발생시키고, 이는 수학의 위계성과 결합하여 수학학습부진을 가중시킨다. 또한 수학에 대한 교사의 부정적인 성향은 학생들에게 전달되어 수학불안, 자신감 상실 등을 야기하여 수학학습부진으로 이어진다. 사회문화 변인은 가정, 학교, 사회와 관련된 요인으로서 가정결손이나 경제적 환경과 수학을 잘 못해도 괜찮다는 등의 사회적인 수용적 분위기 등이 포함된다. 부모의 수학에 대한 가치관과 가정에서의 성취압력, 학습에 대한 조력, 학습관과 같은 양육 방식도 학습부진의 원인이 된다. 마지막으로 수학 변인에는 수학 자체의 학문적 성격에서 비롯하며, 수학의 위계성, 직관보다는 논리를 강조하는 특성, 추상화, 일반화, 형식화 과정의 요구, 추상적 언어와 엄밀한 용어 정의 등이 수학학습 부진에 많은 영향을 미친다.
Topic Modeling
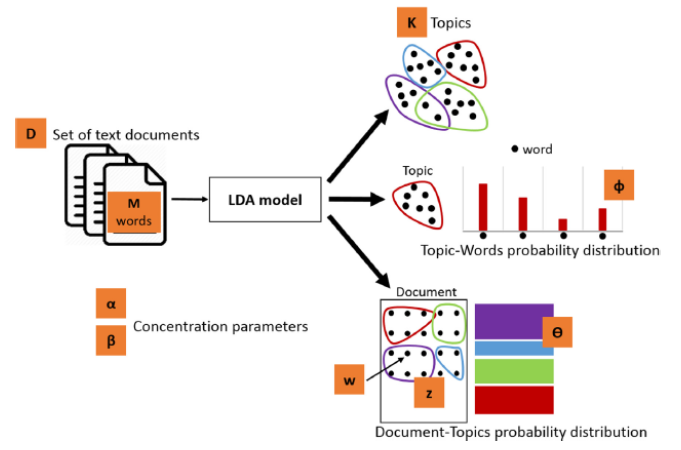
토픽모델링은 비정형화된 텍스트 데이터로부터 의미 있는 정보와 구조를 도출해낼 수 있는 텍스트 마이닝(text mining) 기법의 한 종류로서(Blei & Lafferty, 2009), 문서들을 토픽이라는 집합으로 분류하는 통계적 모델이다(Son & Lee, 2020). 대량의 데이터를 연구자가 일일이 처리하는데 걸리는 시간을 줄여주며, 데이터 이면에 숨겨진 의미를 발견할 수 있다. 토픽 모델링의 여러 모델 중 일반적으로 가장 널리 활용되는 기법은 잠재 디리클레 할당(Latent Dirichlet Allocation; 이하 LDA)이다. LDA는 대량의 문서 집합을 처리하기에 용이하고 텍스트로부터 의미 있는 설명과 구문을 정확하게 얻을 수 있다(Nabli et al., 2018). 또한 LDA는 하나의 문서가 여러 개의 잠재적인 토픽으로 구성되어 있다고 가정하며, 관측가능한 단어의 패턴을 통해 특정 토픽의 특성을 추론해 나간다(Blei et al., 2003). Fig. 1은 LDA 수행과정을 시각화한 모델이다.
이 과정을 자세하게 알아보자. 문헌에 어떤 토픽이 할당되어 있는 파악하려면 관측 가능한 변수 wd, n으로부터 잠재 변수를 추론해 나가야 한다. 그러나 정확한 확률 분포가 가정되지 않으므로 매개변수 α, β와 관측 가능한 변수 wd, n을 통해 잠재 변수의 확률 분포를 추론해 나간다. Fig. 1에서 K개의 토픽이 정해지면 관측 가능한 한 문헌의 단어들 w(i, j)은 매개변수 α, β에 의해 결정되는 단어의 토픽할당 Z (i, j)에 의해 단어들의 토픽 K에 대한 확률 분포 Φ(K)가 결정된다. 예컨대, 토픽 개수를 4개로 정했다면 단어 ‘error’는 토픽 1에 속할 확률 60%, 토픽 2에 속할 확률 30%, 토픽 3에 속할 확률 7%, 토픽 4에 속할 확률 3%와 같은 형태로 토픽-단어 확률 분포가 결정되는 것이다. 이 과정이 M번 반복되면 4개의 토픽으로 구성된 단어의 집합을 가진 하나의 문헌이 생성되며(Θ(i)), D개의 문헌 집합에 반복적으로 수행되면 문헌들이 어떤 토픽에 속하는지에 대한 확률 분포가 결정된다. LDA는 앞서 기술한 과정을 역으로 실시하며, 관측 가능한 변수인 단어 w(i, j)으로부터 문헌의 토픽 확률 분포 θd를 추정하는 방법이다(Blei et al., 2003).
이처럼 토픽모델링은 단어 간의 유사성을 확률 분포를 통해 토픽을 분류하므로 연구자의 주관성이 배제되는 특징을 지닌다(Son & Lee, 2020). 따라서 연구자가 선정한 분석틀이 아니라 관측된 단어의 패턴을 따라 추론하므로 더욱 강력한 모델링의 구축이 가능하다(Blei et al., 2003).
D : Set of text documents
K : The number of topics
M : Set of words in a document
Z (i, j) : The topic assignment for w(i, j)
Φ(K) : The word distribution of topic k
Θ(i) : The topic distribution of document i
w(i, j): The jth word of the ith document
α : The Dirichlet-prior concentration parameter of the per-document topic distribution
β : The Dirichlet-prior concentration parameter of the per-topic word distribution
Research Methods
Data Collection
분석 대상은 국내에서 발간된 학위논문 및 학술지에 게재된 논문 전체로서, 이를 위해 한국교육학술정보원에서 제공하는 학술연구정보서비스(Research Information Sharing Service; [RISS])를 활용하였다. RISS 데이터베이스에서 ‘수학’과 ‘부진아’를 키워드로 사용하여 1,174편의 논문 서지정보를 수집하였으며, 이 중 수학이 아닌 교과나 범교과 논문, 수학학습부진아가 아닌 수학학습장애에 대한 연구를 제외하고 최종적으로 782편의 논문을 선정하였다. 선정된 논문의 게재년도는 1975년부터 2019년까지였으나, 1980년 이전 연구가 1편에 불과하므로 이를 제외하고 1980년부터 2019년까지의 논문을 분석하였다.
토픽모델링 연구에서는 일반적으로 서지정보들 중 초록을 주로 활용한다. 이는 초록이 연구의 목적과 문제, 연구를 통해 발견한 사실과 가치 있는 내용을 포함하기 때문이다(Chen et al., 2020; Griffiths & Steyvers, 2004). 따라서 본 연구에서는 제목, 키워드, 저자 등의 정보는 분석 대상에서 제외하고 분석의 통일성을 꾀하기 위해 영문 초록만을 분석하였다.
Pre-Processing
전처리 과정은 R(version 4.0.2) 프로그램을 활용하였다. 먼저 수집한 데이터로부터 단어를 정제하는 과정을 수행하였다. 이를 위해 일상적으로 사용되는 the, as, a, is 등과 같은 불용어(stop-word)를 제거하고, 대문자를 모두 소문자 형태로 변환하였다. 또한 ‘number’가 ‘a number of’로 활용되는 경우와 같이 단어가 중의적으로 활용되는 경우를 찾아 제거하였다. 이 후, 빈도수가 다른 단어들에 비해 매우 높은 이상치(outlier) 단어들을 제거하였다. 예컨대, ‘student’, ‘teacher’, ‘math’와 같은 단어들은 모든 논문마다 등장하는 이상치 단어들이다. 만약 이러한 단어들을 삭제하지 않고 토픽모델링을 수행할 경우, 주요 키워드로 출현하게 되므로, 이를 방지하기 위해 ‘student’, ‘teacher’, ‘underachiever’, ‘math’, ‘learn’, ‘teach’의 여러 품사 형태를 찾아 제거하였다.
Determine an Appropriate Number of Topics
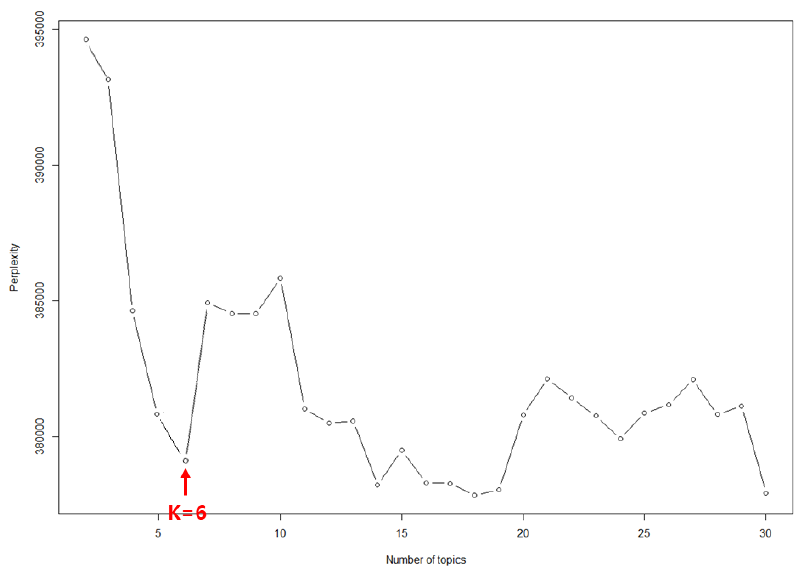
토픽모델링 수행은 R의 ‘topicmodels’ 패키지를 활용하였으며, 매개변수 는 0.1로 설정하고 깁스 샘플링(gibbs sampling) 방식으로 1,000회를 반복하였다. 토픽모델링에서 토픽의 개수는 연구자가 지정해야하며, 이에 대한 연구자들 간의 통일된 견해는 없다. 그러나 토픽모델링 연구에서 가장 많이 활용되는 방법은 혼잡도(perplexity; Blei et al., 2003)이다. 혼잡도 지수는 토픽들 간의 분류 정도를 판단하는 지표로서 값이 적을수록 적절한 모델을 의미한다(Blei et al., 2003). Inglis & Foster (2018)는 토픽 수가 늘어날수록 혼잡도 지수는 감소하므로 기울기의 변화가 급격하게 변화하는 지점을 선택할 것을 주장하였다. 이에 본 연구에서는 값을 2에서 30까지로 설정하고 혼잡도의 변화 추이를 살펴보았다. Fig. 2에서 나타나듯이, 가 6을 기준으로 혼잡도 지수의 기울기가 급격하게 변화하므로 이를 적합한 토픽 개수로 선정하였다.
선정한 토픽 개수에 따라 전처리 과정을 거친 데이터에 대한 LDA를 수행하고 각 토픽에 나타나는 상위 10개 단어와 원문을 검토하여 적절한 토픽 명을 부여하였다. 예컨대, 추출된 토픽의 상위 10개 단어 집합이 {errors, error, level, types, grade, calculation, subtraction, addition, operation, correction}로 출현한 경우 ‘수학학습부진아의 오류’로 토픽 명을 부여하였다.
Results
Analysis Result of LDA
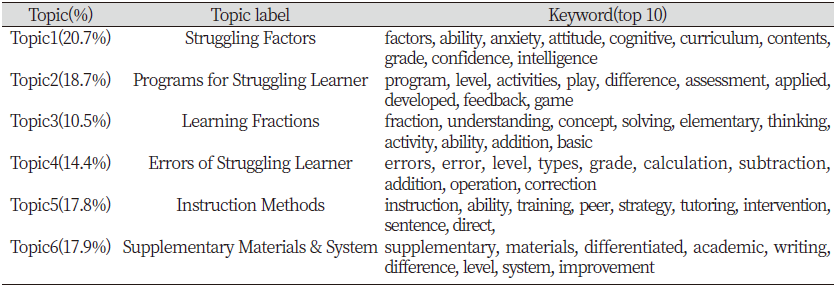
국내 수학학습부진아 연구 데이터에 대한 LDA 수행 결과, 6개의 토픽이 Table 1과 같이 추출되었다. 토픽의 키워드들은 LDA 알고리즘을 따라 단어의 토픽 할당 확률인 ‘beta’값이 가장 높은 상위 10개의 단어를 나열한 것이다.
토픽 모델링 분석 결과, 국내 수학학습부진아 연구는 ‘부진 요인’, ‘수학학습부진아를 위한 프로그램’, ‘분수 학습’, ‘수학학습부진아의 오류’, ‘교수 방법’, ‘보충 자료 및 시스템’으로 구분할 수 있었다. 이 중 ‘Topic1: 부진 요인’은 20.7%로서 가장 많은 비중을 차지했으며, ‘Topic3: 분수 학습’은 10.5%로 가장 낮은 비중을 차지했다. 도출된 토픽들의 세부적인 내용을 살펴보기 위해 문서의 토픽 할당 확률인 ‘gamma’를 기준으로 대표 논문을 선정하였으며, 구체적인 내용은 Table 2와 같다.
토픽별 내용을 살펴보면 다음과 같다.
첫째, ‘부진 요인’은 불안(anxiety), 태도(attitude), 인지(cognitive), 교육과정(curriculum), 학습 내용(contents), 자신감(confidence), 지능(intelligence)과 같이 수학학습부진아들에게 영향을 미치는 다양한 요인에 관한 연구로서, 대표적인 연구는 수학 기피요인을 검사하고 분류하여 치유 효과를 살펴본 Park (2003)의 ‘수학 교과 학습 부진의 유형별 요인에 따른 효과적인 대처 방안’으로 나타났다.둘째, ‘수학학습부진아를 위한 프로그램’은 활동(activities), 놀이(play), 평가(assessment), 게임(game)과 같은 키워드를 포함하며, 수학학습부진아의 학습 개선을 위한 프로그램 개발과 이에 대한 효과를 검토한 연구들이다. 대표적인 연구는 문헌연구를 통해 수학학습부진아의 특성과 원인을 살펴보고 수학 학습 프로그램을 개발하여 그 효과를 살펴본 Song (2001)의 ‘수학 학습 부진아의 학습 태도 개선을 위한 학습 프로그램 개발 연구’로 나타났다.
둘째, ‘수학학습부진아를 위한 프로그램’은 활동(activities), 놀이(play), 평가(assessment), 게임(game)과 같은 키워드를 포함하며, 수학학습부진아의 학습 개선을 위한 프로그램 개발과 이에 대한 효과를 검토한 연구들이다. 대표적인 연구는 문헌연구를 통해 수학학습부진아의 특성과 원인을 살펴보고 수학 학습 프로그램을 개발하여 그 효과를 살펴본 Song (2001)의 ‘수학 학습 부진아의 학습 태도 개선을 위한 학습 프로그램 개발 연구’로 나타났다.
셋째, ‘분수 학습’은 주로 초등 수준의 수학학습부진아 연구에 초점이 맞추어져 있으며, 분수에 대한 이해(understanding), 문제 해결(solving), 사고(thinking), 능력(ability) 등의 키워드를 포함한다. 대표적인 연구는 분수의 개념적 이해가 분수의 덧셈 학습으로의 전이 정도를 살펴보고 이에 대한 시사점을 제시한 Ha (2010)의 ‘수학학습부진아를 대상으로 분수의 개념적 이해에서 분수의 덧셈으로의 전이 가능성 연구’로 나타났다.
넷째, ‘수학학습부진아의 오류’는 주로 계산(calculation)이나 연산(operation) 과정에서 나타나는 수학학습부진아의 오류 유형(type)을 분석하고 이를 교정(correction)하기 위한 목적으로 시행된 연구들이다. 대표적인 연구는 고등학교 수학학습부진아의 수학 내용 영역별 오류 유형을 분석하고 향후 지도 방안에 대한 시사점을 제시한 Kwon et al. (2015)의 ‘내용 영역에 따른 수학학습 부진아의 성취수준 및 오류유형 분석’으로 나타났다.
다섯 째, ‘교수 방법’은 동료(peer) 교수, 튜터링(tutoring), 직접(direct) 교수 등과 같이 여러 교수 전략(strategy)을 활용한 교수 방법을 적용하여 수학학습부진아의 개선을 도모하는 연구들이다. 대표적인 연구는 자기교시 훈련이 수학학습부진아의 수학 문장제 해결능력에 미치는 영향을 분석한 Lee (2007)의 ‘자기교시훈련이 수학 학습부진아의 수학 문장제 해결능력에 미치는 효과’로 나타났다.
여섯 째, ‘보충 자료 및 시스템’은 주로 수준별 보충 자료(differentiated supplemental materials)를 제공하거나 지원 시스템(system)의 구축을 통해 수학학습부진아의 개선(improvement)을 도모하는 연구이다. 대표적인 연구는 수준별 보충 자료의 활용이 수학학습부진아의 학습 태도와 성취도에 미치는 영향을 분석한 Kim & Song (2012)의 ‘수준별 보충 자료를 활용한 학습부진아의 수학 학습태도 및 학업성취도 향상에 대한 연구’로 나타났다.
Analysis Result of Time-series
Overall Research Trends
시간의 흐름에 따라 수학학습부진 연구 동향의 추이가 어떻게 변화하는지 살펴보기 위해 시계열에 따른 연구 동향을 분석하였다. 먼저 전반적인 연구 동향을 살펴보기 위해 1980년부터 2019년까지의 연구들을 10년 단위로 구분하고 대표적인 키워드의 출현 빈도를 살펴보았다. 시기별로 단어의 빈도수를 기준으로 상위 100개의 단어를 추출하여 Word Cloud로 시각화하였다. 구체적인 결과는 Fig. 3과 같으며, 단어의 크기는 빈도를 의미한다.
Fig. 3에서 나타나듯이, 시기별 빈도수가 가장 많은 단어는 자료(materials), 문제(problem), 프로그램(program), 태도(attitude)로 나타났다. 이러한 단어들은 넓은 관점에서 보았을 때, 해당 시기의 수학학습부진아 연구를 대표하는 단어들이며 주요한 연구 주제였음을 의미한다(Son & Lee, 2020). 이러한 관점에서 보았을 때, 국내 수학학습부진아 연구의 흐름은 1980년대에는 자료의 제공, 1990년대에는 문제 해결 및 제시, 2000년대에는 프로그램 개발 및 적용, 2010년대에는 학습 태도 개선 순으로 연구의 흐름이 변화해왔음을 유추해볼 수 있다.
Research Trends for Each Topic
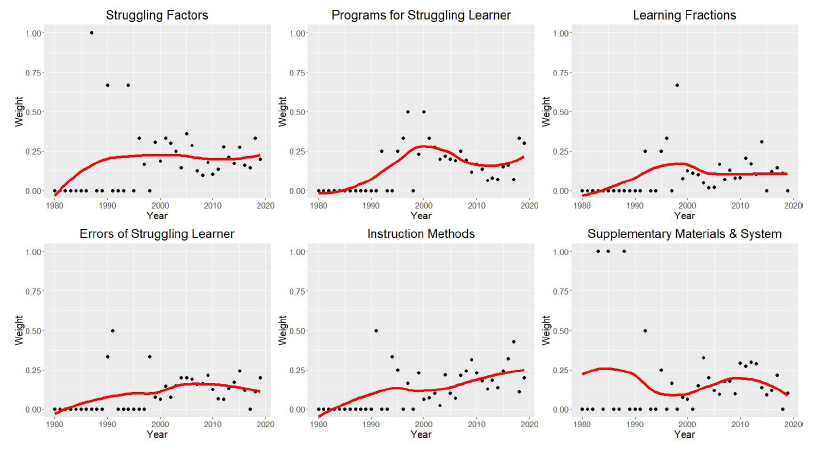
시계열에 따른 토픽 비중의 변화를 파악하기 위해 1980년부터 2019년까지의 데이터를 곡선추정 단순회귀선으로 나타내고 그 변화를 살펴보았다. 구체적인 결과는 Fig. 4와 같으며, 가로축은 년도, 세로축은 해당 토픽이 특정 년도에서 차지하는 비중을 의미한다.
수학학습부진아 연구의 변화 추이를 살펴본 결과, 관련 연구가 출현하기 시작한 1980년대 이래로 1990년까지 증가하는 추세를 전반적으로 나타냈으며 1990년 이후로 토픽에 따라 증감의 변화는 차이를 보였다. 먼저 1990년 이래로 비중이 유지되는 토픽은 ‘부진 요인’과 ‘분수 학습’이며, ‘분수 학습’의 경우 2000년까지 꾸준히 증가하다가 잠시 감소하는 경향을 보인 후 다시 유지되는 추이를 보였다. 비중이 꾸준히 증가하는 토픽은 ‘수학학습부진아의 오류’와 ‘교수 방법’으로 나타났으며, 일부 구간에서 약간의 증감은 보이지만 전반적으로 꾸준히 증가하는 추세를 보였다. 다른 토픽들에 비해 비중의 변화가 큰 토픽은 ‘수학학습부진아를 위한 프로그램’과 ‘보충 자료 및 시스템’으로 나타났다. ‘수학학습부진아를 위한 프로그램’은 시계열에 따라 전반적으로 비중이 증가하는 경향을 보인다. 그러나 2000년까지 연구의 비중이 증가하다가 2010년까지 다시 감소한 후 약간의 증가 추세를 보였다. 또한 ‘보충 자료 및 시스템’은 2000년부터 2010년까지 연구의 비중이 증가하다가 이후 2019년까지 다시 감소하는 경향을 보였다.
Hot & Cold Topic
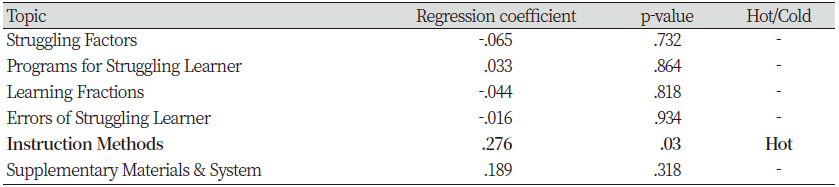
토픽별 시계열 변화의 통계적으로 유의미함을 검증하기 위해 토픽별 비중에 대한 선형회귀분석을 수행하였다. 1990년 이래로 수학학습부진아 연구가 본격적으로 시작되었으므로, 1980년대를 제외하고 1990년부터 2019년까지의 기간에 대한 시계열 회귀분석을 실시하였다. 그 결과, 유의확률(p-value) 값이 95% 유의수준에서 유의미하고 회귀계수 값이 양수(+)인 경우 Hot 토픽, 음수(-)인 경우 Cold 토픽, 유의미한 결과가 도출되지 않은 토픽은 Neutral 토픽으로 분류하였다(Griffiths & Steyvers, 2004). Hot 토픽은 시계열에 따라 연구의 비중이 통계적으로 유의하게 증가한 토픽, Cold 토픽은 연구의 비중이 통계적으로 유의미하게 감소된 토픽을 의미한다. Table 3은 수학학습부진아 연구 토픽들의 시계열 회귀분석 결과이며 Hot 토픽은 ‘Hot’, Cold 토픽은 ‘Cold’, Neutral 토픽은 ‘-’로 표시하였다.
시계열 회귀분석 결과, ‘교수 방법’이 Hot 토픽으로 나타났으며 나머지 5개의 토픽은 Neutral 토픽으로 드러났다. 또한 다른 토픽들에 비해 수학학습부진아에 대한 ‘교수 방법’ 연구가 최근 많이 이루어지고 있음을 반증하는 결과이기도 하다. 한 가지 주목할 점은 곡선추정 단순회귀선에서 1990년대 이후 증가하는 경향을 보인 ‘수학학습부진아의 오류’는 통계적으로는 유의미한 결과를 나타내지 않았다는 점이다. 이는 일부 구간에서 연구 비중이 감소하는 경향이 나타났으므로, 연도별 데이터의 값을 선형 회귀선으로 나타냈을 때 유의미한 결과를 도출하지 못한 것으로 판단된다.
Conclusion & Implication
본 연구는 1980년부터 2019년까지 국내 수학학습부진아 연구 동향을 파악하고 시계열에 따라 어떤 비중 변화를 보였는지 살펴보았다. 그동안 수학학습부진아 연구 동향을 살펴본 연구가 거의 수행되지 않았고 토 픽모델링을 사용하여 토픽별 변화를 세밀하게 다룬 연구가 없다는 점에서 의의가 있다. 분석 결과를 통해 도 출한 결론은 다음과 같다.
첫째, 수학학습부진아 연구에서 LDA를 통해 도출된 토픽은 6개로 나타났다. LDA 분석 결과(Table 1, 2 참 조), 수학학습부진아 연구는 ‘부진 요인’, ‘수학학습부진아를 위한 프로그램’, ‘분수 학습’, ‘수학학습부진아의 오류’, ‘교수 방법’, ‘보충 자료 및 시스템’의 6개의 토픽으로 분류되었다. 이 중 부진 요인에 대한 비중이 20.7% 로 가장 높았으며, 이는 수학학습부진아가 지니는 복합적인 부진 요인을 밝히고 개선하는 연구가 많이 이루 어져 왔음을 의미한다. 또한 주목할 점은 분수 학습이 그 비중은 10.5%로 가장 낮았지만 하나의 독립적인 토 픽으로 출현하였다는 점이다. 이는 수학학습부진아 연구가 수학학습 부진의 원인인 수학 변인 중 분수 학습 에 집중되어 왔음을 의미한다.
둘째, 수학학습부진아 연구에서 주목한 연구 주제는 시기별로 다르게 나타났다. 시계열에 따른 전반적인 연구 동향을 분석한 결과에 따르면(Fig. 3 참조), 1980년대부터 2010년대까지 ‘자료’, ‘문제’, ‘프로그램’, ‘태도’ 가 시기별로 빈도수가 가장 많은 단어로 추출되었다. 이는 수학학습부진아 연구가 특정 연구 주제에 시기별 로 집중되는 경향이 있으며, 수학학습부진아의 학업 성취 수준의 향상이라는 목적은 동일하지만 구체적인 방법 면에서 차이를 보임을 의미한다. 즉, 1980년대에는 보충 학습 자료의 제공, 1990년대에는 문제 해결 및 제시, 2000년대에는 프로그램 개발 및 적용, 2010년대에는 학습 태도 개선의 과정을 통해 수학학습부진아를 개선하려는 노력을 기울여 왔음을 알 수 있다.
셋째, 수학학습부진아 연구의 각 토픽들은 시계열의 변화에 따라 증감 변화가 다르게 나타났다. 곡선추정 회귀선을 통해 시계열 토픽 비중 변화를 살펴보았을 때(Fig. 4 참조), ‘부진 요인’과 ‘분수 학습’은 비중이 꾸준 히 유지되는 경향을 보였으며, 이 중 ‘부진 요인’은 시간의 변화에도 불구하고 약 25%의 연구 비중을 지속적 으로 유지하는 경향을 보였다. 또한 ‘수학학습부진아의 오류’와 ‘교수 방법’은 그 비중이 시계열에 따라 꾸준 히 증가하는 경향을 보였으며, ‘수학학습부진아를 위한 프로그램’과 ‘보충 자료 및 시스템’은 비중의 변화가 시계열에 따라 큰 폭으로 변화하는 경향을 나타냈다. 선형회귀분석을 통해 통계적으로 유의미한 증가 경향 을 보인 Hot 토픽은 ‘교수 방법’으로 나타났다. 이는 수학학습부진 연구가 주로 지도 방법 개선과 새로운 지도 프로그램 개발 관점에서 이루어져 왔다고 주장한 Park & Oh (2013)의 연구와 맥락을 함께 한다.
본 연구의 결과를 통해 도출한 수학학습부진아 연구에 대한 시사점은 다음과 같다.
첫째, 수학과의 다른 영역에 대한 수학학습부진아 연구가 확산되어야 한다. LDA 수행 결과, 수학 개념 중 ‘분수 학습’만이 독립적인 토픽으로 출현하였다. 분수 학습에 수학학습부진 연구가 집중된 이유를 살펴보면, 학습의 위계를 지니는 수학교과의 특성상 초등학교에서의 부진이 후속 학습에 영향을 미치며, 분수는 초등 학교 수준에서 학습하는 수학 개념 중 학생들이 학습하는데 가장 어려움을 겪는 개념 중 하나이기 때문이다 (Kim & Choi, 2012). 이러한 특성을 고려했을 때, 그동안의 수학학습부진아 연구가 분수 학습에 집중되어 온 것은 당연해 보인다. 그러나 수와 연산, 기하, 확률과 통계 등의 다른 수학 영역 또한 독자적인 학습 계열과 구 조를 지니므로 수학학습부진의 한 요인으로 작용될 수 있다. 그동안 여러 수학 개념에 대한 수학학습부진아 연구가 이루어져왔으나 분수 학습에 비해 저조한 실정이므로, 특정 수학 주제에 집중된 연구보다는 여러 수 학 영역에 대한 연구를 통해 수학학습부진아의 특성을 밝히고 개선하는데 노력을 기울일 필요가 있다.
둘째, 수학학습부진아의 진단에 대한 연구가 확산될 필요가 있다. Kim (2001)은 학습부진 학생들의 원인을 분석하거나 그 유형을 분류하여 재배치하는 과정이 없이 진단과 동시에 시행되는 교육적 처치는 오히려 학 습의 효율성을 떨어뜨린다고 강조하였다. 이처럼 수학학습부진아의 개선을 위해 초기 진단과 선별이 중요 함에도 불구하고 도출된 토픽과 키워드에는 진단과 선별에 관한 내용은 출현하지 않았다. 이는 수학학습부 진아 연구가 수학학습부진아의 진단보다는 부진 요인과 오류, 보충 자료 제공 등의 개선 과정에 집중되어 있 음을 의미한다. 따라서 향후 연구에서는 수학학습부진아의 초기 진단과 그 원인을 파악하여 부진 유형을 구 체적으로 분류하고 처치할 수 있는 방안에 대한 연구가 이루어져야할 필요가 있다.
셋째, 수학학습부진의 원인이 되는 사회문화 변인에 대한 연구가 확산될 필요가 있다. LDA를 통해 도출된 토픽들과 키워드를 살펴보면, 주로 학생 변인, 수업 변인, 수학 변인에 대한 내용들이었으며 사회문화 변인 에 대한 토픽과 키워드는 나타나지 않았다. 그러나 수학학습부진의 원인은 다양하고 복합적으로 작용한다 는 점을 고려할 때, 학습자의 특성과 수업, 그리고 수학 내용에 대한 연구뿐만 아니라 수학학습부진아의 가 정환경과 부모의 사회 경제적 지위에 의한 교육 격차 등과 같은 사회문화 변인을 함께 고려한 연구가 수행될 필요가 있다.
본 연구는 1980년부터 2019년까지 국내 수학학습부진아 연구의 동향을 분석하기 위해 토픽 모델링을 활용 하여 연구 흐름을 조망하고 수학교육 평가 연구의 후속 과제를 제언하였다. 본 연구 결과가 추후 수학학습부 진아 연구 발전에 유용한 도움이 되기를 기대한다.
Authors Information
Son, Taekwon: Daegu Dong-do Elementary School, Teacher, First Author ORCID: https://orcid.ogr/0000-0003-4497-9188
Ahn, Do-Yeon: Cheonan Cheong-dang Elementary School, Teacher, Co-author
Yoo, Sung-Yoon: Daejeon Dong-hwa Elementary School, Teacher, Co-author
Lee, Kwnag-Ho: Korea National University of Education, Professor, Corresponding Author ORCID: https://orcid.org/0000-0001-5444-8423